최장 증가 부분 수열이라고 불리는 Longest Increasing Subsequence는 $O(NlogN)$ 에 구할 수 있다.
많은 블로그에서 이분 탐색을 활용한다라는 해결책을 제시하는데, 해당 풀이를 도출해나가는 과정을 자세히 작성하고자 한다.
알고리즘 강의를 들으며 정리한 내용으로, 오류가 있을 수 있습니다. 발견하신다면 댓글로 알려주시면 감사하겠습니다 🙌
0. Longest Increasing Subsequence
LIS는 주어진 수열에서 가장 긴 증가하는 부분 수열이다. 주어진 수열을 $S$ 라고 하고, LIS를 $L$ 라고 하자. 이때,
$L$ 의 원소들이 $S$에서 연속적으로 존재해야할 필요는 없다.
LIS는 어떻게 구해야 할까?
1. Naive
간단히 생각하면, 모든 경우의 수를 다 따져보면서 구할 수 있다. 모든 부분 수열을 확인해야 하므로 각 원소의 포함 여부를 알아야 한다. 포함된 원소로 만든 부분 수열 $A$ 가 $1 \le i \le len(A)$ 인 모든 $i$에 대해서 $A_i < A_{i+1}$ 를 만족하는지도 확인해야 한다. $N$ 개의 원소는 포함/미포함 상태를 가지므로 $2^N$ 의 경우의 수가 있고, 각 부분 수열이 위 조건을 만족하는지 확인하는 데 $O(N)$ 이 소요된다. 최종 시간복잡도는 $O(N2^N)$ 이다.
2. Dynamic Programming
유명한 $O(N^2)$ 풀이로 DP를 이용하는 방법이 있다. $dp_i$ 를 $i$ 번째 원소로 끝나는 부분 수열이라고 하자. 그럼 아래와 같은 비교적 간단한(?) 점화식을 구할 수 있다.
$dp_i = S_k < S_i, 1 \le k \le i-1$ 인 $k$ 에 대해 $max(dp_k)+1$
모든 원소에 대해서 해당 원소를 마지막 원소로 가지는 부분 수열을 도는 데 $N$, 각 부분 수열을 찾아내는 데 $O(N)$ 으로 $O(N^2)$ 의 시간복잡도를 가진다.
https://www.acmicpc.net/problem/11053 에서 문제를 확인할 수 있다. 제한이 $1\,000$ 이기 때문에, $O(N^2)$ 에 무난하게 돌아간다.
11053번: 가장 긴 증가하는 부분 수열
수열 A가 주어졌을 때, 가장 긴 증가하는 부분 수열을 구하는 프로그램을 작성하시오. 예를 들어, 수열 A = {10, 20, 10, 30, 20, 50} 인 경우에 가장 긴 증가하는 부분 수열은 A = {10, 20, 10, 30, 20, 50} 이
www.acmicpc.net
3. Binary Search
다음과 같은 문제를 보자, $N$ 제한이 $1\,000\,000$ 으로, 앞서 소개한 $O(N^2)$ 풀이는 시간초과를 받는다.
https://www.acmicpc.net/problem/12015
12015번: 가장 긴 증가하는 부분 수열 2
첫째 줄에 수열 A의 크기 N (1 ≤ N ≤ 1,000,000)이 주어진다. 둘째 줄에는 수열 A를 이루고 있는 Ai가 주어진다. (1 ≤ Ai ≤ 1,000,000)
www.acmicpc.net
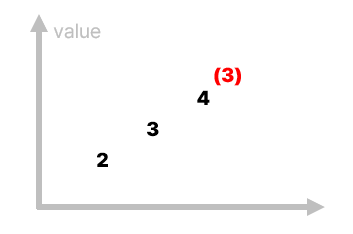
이해를 돕기 위해 그림을 그려 보자. $y$ 축은 값(value)을 나타내고, 빨간 글씨는 해당 원소를 마지막으로 갖는 부분 수열의 길이이다. 배열은 왼쪽부터 오른쪽 순서대로 주어진다고 하자.
1. 길이가 같은 부분 수열이 두 번 등장하는 경우를 생각해 보자. 앞쪽과 뒤쪽 중, 어느 것의 value가 높을까?
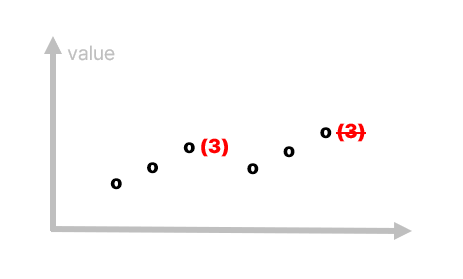
뒤쪽 부분 수열이 더 높은 value를 가지는 경우는 존재하지 않는다. 더 높을 경우, 뒤쪽 부분 수열의 길이는 앞쪽 부분 수열의 길이보다 1 이상 커야 한다.
즉, 같은 길이의 부분 수열이 두번 등장한다면, 같거나 더 낮은 value를 가진다. 같은 길이의 부분 수열들을 통해 LIS를 구축한다면, 부분 수열의 value를 최대한 낮게 가져가는 게 이득이다. 낮은 value를 가지는 부분 수열은 길이가 같다면 항상 오른쪽에 나타나므로, 가장 오른쪽의 value를 기억해두면 된다.
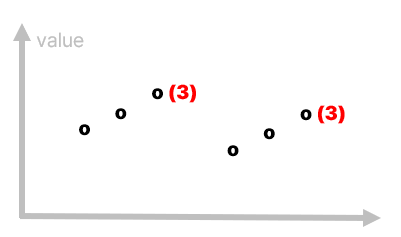
2. 길이가 서로 다른 부분 수열이라면 어떨까?
서로 다른 부분 수열의 길이를 가질 때, 우선 앞쪽이 더 긴 경우, value가 같게 되는 경우는 없다. 뒤쪽 또한 앞쪽 수열의 원소들로 이루어진 부분 수열을 새로 구축할 수 있다.

뒤쪽이 더 긴 경우를 생각해 보면, value가 같게 되는 경우는 있지만, 앞에서 설명했던 방법을 적용하면 앞쪽 부분 수열을 뒤로 넘겨줘야 한다 (가장 오른쪽의 value를 기억한다)

관찰을 통해 몇 가지 정보를 얻었다. 정리하면,
- 길이가 같은 부분 수열의 경우, 더 나중에 나오는 부분 수열을 기억한다.
- 길이가 서로 다른 부분 수열은, 길이가 높을수록 같거나 더 높은 value를 가진다.
위 두 가지 정보를 바탕으로 새로운 배열을 구축해 보자. 해당 배열의 $k$ 번째 자리에는 부분 수열의 길이가 $k$ 인 것 중에서, 가장 오른쪽에 위치한 부분 수열의 value를 저장한다.

다음과 같이 주어진 수열 순서대로 배열을 채워나가던 도중에 새로운 값 6을 만났다고 하자. 빨간색 괄호는 부분 수열의 길이를 나타내고, 높낮이는 value를 나타낸다.
만들어나가는 배열은 비내림차순 정렬되어 있다. 위의 관찰을 바탕으로 규칙에 따라서 배열을 채워나가기 때문이다.
수가 주어지면, 해당 수가 어떤 부분 수열의 가장 끝 자리에 와야 하는지를 찾아내기만 하면 되며, 그 부분 수열의 끝 자리를 새로 들어오는 값으로 대치시켜주면 된다.
6이 들어올 때, 6을 마지막으로 갖도록 만드는 부분 수열의 길이는 5이다. 따라서 배열의 5번째 값을 6으로 바꾸어주면 된다.
배열의 몇 번째 값을 바꿔줘야하는지 알기 위해서 이분 탐색을 활용한다. 이 많은 앞의 과정을 통해서 우리는 이분 탐색을 통해 시간을 줄일 수 있음을 알게 되었다..
배열이 단조로운 것은 참 많은 측면에서 유용하다. 특히나 이분 탐색을 통해 풀이법의 시간복잡도 $O(N)$ 을 $O(logN)$ 으로 줄여준다는 것을 생각하면 정말 강력하다.
'study > algorithm' 카테고리의 다른 글
| [Python] Offline Dynamic Connectivity - 동적 연결성 문제를 오프라인으로 해결하기 (0) | 2022.08.01 |
|---|---|
| [Algorithm | Python] HeavyLight Decomposition (HLD) (0) | 2022.06.22 |
| [파이썬 | Python] 트라이 (Trie) 자료구조 (0) | 2021.05.17 |
