그래프 문제에서, Dynamic Connectivity Problem이라고 하는 것은 다음 세 가지 쿼리를 해결하는 문제를 의미한다.
1. 두 정점 $u$, $v$ 를 잇는 간선을 추가한다
2. 두 정점 $u$, $v$ 를 잇는 간선을 제거한다
3. 정점 $u$ 에서 $v$ 로 도달 가능한지 확인한다
단순하게 1, 3번 쿼리로만 이루어진 문제이거나, 2-3번 쿼리로만 이루어진 문제라면 Disjoint-Set Union(DSU) 자료구조를 사용해서 해결할 수 있다.
간선을 추가하고 제거하면서 그와 동시에 정점 사이에 경로가 있는지 확인하려면.. 꽤나 어려울 것 같다.
이런 식의 문제를 해결하는 방법은 크게 두 가지가 있다고 생각하는데,
하나는 (내가 모르는) 자료구조나 알고리즘을 사용해서 문제를 해결하는 것이고,
다른 하나는 쿼리를 통째로 오프라인으로 가져가서 문제를 해결하는 것이다.
실제로 위 문제의 2, 3번 쿼리만을 사용하는 문제는 쿼리를 받아둔 뒤, 역으로 간선을 이어 나가면서 해결하는 방법이 있다.
이 글에서는 두 번째 방법인, 오프라인으로 동적 연결성 문제를 해결하는 방법을 설명한다.
* 선행지식: Disjoint-Set Union-Find, Stack, Divide-and-Conquer, (Segment tree)
지금까지 배웠던 많은 알고리즘 / 자료구조를 한데 모은 느낌이라, 새로 배우면서도 정말 재미있었다.
우선 각 간선별로 생애주기를 그린다. 시간의 기준은 도달 가능한지를 물어보는 쿼리가 될 것이다. 예를 들어,
(간선1 +) (간선2 +) (간선3 +) (쿼리) (간선1-) (간선4+) (쿼리) (간선3-)
입력이 있었다고 한다면, 아래와 같이 그릴 수 있다. 간선1은 (1, 2)구간, 간선2는 (1, 4)구간동안 존재했다는 의미이다.
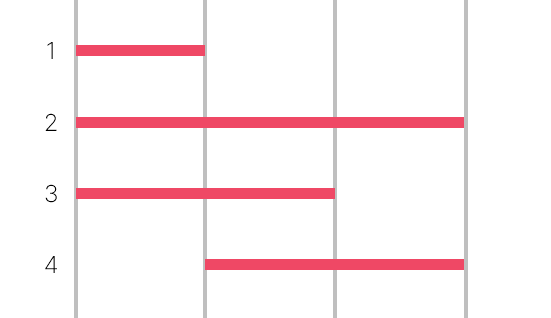
이 문제를 해결하는 것의 핵심은 분할 정복(Divide-and-conquer)이다. 경로를 찾는 쿼리의 개수만큼 구간의 개수도 늘어나므로, 해당 구간을 Segment tree와 같이 나눠준 뒤 각 세그먼트 구간에 간선을 저장해둔다. 위 예시를 세그먼트 구간에 넣은 모습은 아래 그림과 같다.

간선을 세그먼트에 저장하는 코드. 재귀적으로 내려가면서 간선의 구간이 세그먼트의 구간을 포함한다면, 해당 세그먼트 구간에 간선을 저장하도록 한다.
def update(tree_l, tree_r, node, elem_l, elem_r, node_pair):
# s, e: node range, l, r: target range
if tree_r < elem_l or elem_r < tree_l:
return
if elem_l <= tree_l and tree_r <= elem_r:
tree[node].append(node_pair)
return
mid = (tree_l + tree_r) // 2
update(tree_l, mid, node * 2, elem_l, elem_r, node_pair)
update(mid + 1, tree_r, node * 2 + 1, elem_l, elem_r, node_pair)
경로 쿼리 개수를 Q개라고 하자. 문제를 해결하는 데에는 한 번의 함수 호출이면 충분하다.
함수는 query(left, right, node_number) 꼴이다. node_number는 세그먼트 상의 [left, right]에 해당하는 번호이다.
처음에는 query(1, Q, 1)로 호출을 시작한다.
def query(l, r, node):
cnt = 0
for a, b in tree[node]:
cnt += uf.merge(a, b)
if l == r:
print(1 if uf.find(queries[l][0]) == uf.find(queries[l][1]) else 0)
uf.revert(cnt)
return
mid = (l + r) // 2
query(l, mid, node*2)
query(mid+1, r, node*2+1)
uf.revert(cnt)
호출은 다음과 같은 단계들로 이루어진다. 본격적인 분할정복이 이 함수에서 나타난다.
query(left, right, node):
1. tree[node]에 해당하는 간선들은 모두 [left, right]상에서는 존재하는 간선이므로, 간선으로 연결된 정점 합침 (union 연산)
2. 만약 left == right 이면 left번째 쿼리의 $u$, $v$가 연결되었는지 확인 (find 연산)
(간선들의 시간은 경로 확인 쿼리에 따라 흘러간다. left == right일 경우에는 left번째 경로 쿼리이므로 연결을 확인한다. 또한 아래 3-1에서 left ~ mid를 먼저 호출하므로 항상 쿼리 순서대로 확인한다는 것을 알 수 있다)
3 - 1. query(left, mid, node*2) 호출
3 - 2. query(mid+1, right, node*2+1) 호출
4. 1에서 union한 간선들을 다시 복구
이 때 union한 간선을 다시 복구하기 위해서는 스택과 Rank compression을 활용한다. (아이디어가 정말 멋있다)
- Union할 때, Path compression 대신 Rank compression을 활용한다. Rank를 사용하면 직전의 상황을 곧바로 롤백할 수 있다.
- Union할 때, 스택에 간선 정보를 push, 복구할 때 스택의 정보를 pop하며 복구한다.
class DSU:
__slots__ = "p", "rank", "stk"
def __init__(self, N):
self.rank = [0] * (N+1)
self.p = [x for x in range(N+1)]
self.stk = []
def find(self, x):
if self.p[x] == x:
return x
return self.find(self.p[x])
def merge(self, a, b):
a, b = self.find(a), self.find(b)
if a == b:
return 0
if self.rank[a] < self.rank[b]:
a, b = b, a
self.stk.append((a, b, self.rank[a] == self.rank[b]))
self.p[b] = a
self.rank[a] += self.rank[a] == self.rank[b]
return 1
def revert(self, cnt):
for _ in range(cnt):
a, b, flag = self.stk.pop()
self.p[b] = b
self.rank[a] -= flag
해당 테크닉을 사용하는 문제들
16911번: 그래프와 쿼리
첫째 줄에 정점의 개수 N(2 ≤ N ≤ 100,000)과 쿼리의 개수 M(1 ≤ M ≤ 100,000)이 주어진다. 둘째 줄부터 M개의 줄에 쿼리가 한 줄에 하나씩 주어진다.
www.acmicpc.net
16912번: 트리와 쿼리 12
첫째 줄에 정점의 개수 N(2 ≤ N ≤ 100,000)과 쿼리의 개수 M(1 ≤ M ≤ 100,000)이 주어진다. 둘째 줄부터 M개의 줄에 쿼리가 한 줄에 하나씩 주어진다. 쿼리의 수행 결과가 포레스트인 입력만 주어진
www.acmicpc.net
정답 코드:
import sys
input = lambda: sys.stdin.readline().rstrip()
mis = lambda: map(int, input().split())
INF = float('inf')
from dataclasses import dataclass
@dataclass
class Edge:
u: int
v: int
start: int
end: int
class DSU:
__slots__ = "p", "rank", "stk"
def __init__(self, N):
self.rank = [0] * (N+1)
self.p = [x for x in range(N+1)]
self.stk = []
def find(self, x):
if self.p[x] == x:
return x
return self.find(self.p[x])
def merge(self, a, b):
a, b = self.find(a), self.find(b)
if a == b:
return 0
if self.rank[a] < self.rank[b]:
a, b = b, a
self.stk.append((a, b, self.rank[a] == self.rank[b]))
self.p[b] = a
self.rank[a] += self.rank[a] == self.rank[b]
return 1
def revert(self, cnt):
for _ in range(cnt):
a, b, flag = self.stk.pop()
self.p[b] = b
self.rank[a] -= flag
def update(tree_l, tree_r, node, elem_l, elem_r, node_pair):
# s, e: node range, l, r: target range
if tree_r < elem_l or elem_r < tree_l:
return
if elem_l <= tree_l and tree_r <= elem_r:
tree[node].append(node_pair)
return
mid = (tree_l + tree_r) // 2
update(tree_l, mid, node * 2, elem_l, elem_r, node_pair)
update(mid + 1, tree_r, node * 2 + 1, elem_l, elem_r, node_pair)
def query(l, r, node):
cnt = 0
for a, b in tree[node]:
cnt += uf.merge(a, b)
if l == r:
print(1 if uf.find(queries[l][0]) == uf.find(queries[l][1]) else 0)
uf.revert(cnt)
return
mid = (l + r) // 2
query(l, mid, node*2)
query(mid+1, r, node*2+1)
uf.revert(cnt)
N, Q = mis()
# Disjoint-Set merge by rank, 1-based
# Use this data structure since the edges are bidirectional
uf = DSU(N)
# Edge management
time_map = {}
all_edges = [None] * Q
finished_edges = []
# Queries Management
queries = [None]
query_count = 0
tree = [[] for _ in range(Q*4)] # Segments
for i in range(Q):
c, a, b = mis()
if a > b: a, b = b, a # make a < b
if c == 1: # Add an Edge
time_map[(a, b)] = i
all_edges[i] = Edge(a, b, query_count+1, INF)
elif c == 2: # Delete an Edge
t = time_map.pop((a, b))
all_edges[t].end = query_count
finished_edges.append(all_edges[t])
else:
query_count += 1
queries.append((a, b))
# (s, INF) -> (s, query_count) for leftover edges
for i in time_map:
e = all_edges[time_map[i]]
e.end = query_count
finished_edges.append(e)
for i in finished_edges:
i: Edge
update(1, query_count, 1, i.start, i.end, (i.u, i.v))
query(1, query_count, 1)
아래는 활용 문제 (생각보다 어려운 아이디어를 사용하는 것 같았는데, D5 -> D4만큼의 난이도가 있지는 않았나 보다)
16695번: The Bridge on the River Kawaii
In a very distant land called Midsommer, there is a cute little river delta. Deep purple acid flows in the river, so it is impossible to swim there. There are several islands in the delta and bridges connecting some pairs of them. Every bridge is assigned
www.acmicpc.net
이미 알고 있는 자료구조나 알고리즘을 활용해서 새로운 문제 푸는 방법을 만드는 게 참 신기하다. 특히나 공부하면서 분할정복이 진짜 멋진 테크닉인 것도 다시 알게 됐다..
공부하면서 참고한 것
https://en.wikipedia.org/wiki/Dynamic_connectivity
https://blog.naver.com/kdr06006/222079403088
'study > algorithm' 카테고리의 다른 글
| Longest Increasing Subsequence (LIS)를 NlogN에 구하기 (0) | 2022.11.03 |
|---|---|
| [Algorithm | Python] HeavyLight Decomposition (HLD) (0) | 2022.06.22 |
| [파이썬 | Python] 트라이 (Trie) 자료구조 (0) | 2021.05.17 |
![[Python] Offline Dynamic Connectivity - 동적 연결성 문제를 오프라인으로 해결하기](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FZaqgh%2FbtrICPaKREd%2FAAAAAAAAAAAAAAAAAAAAAANiKpbqCwCcYUKjyxKdPEhX6pT1C32r4P9LJ2j3Eoh3%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1772290799%26allow_ip%3D%26allow_referer%3D%26signature%3D56Eqw1WTXmDo%252BQKIAHem3nx7c2U%253D)